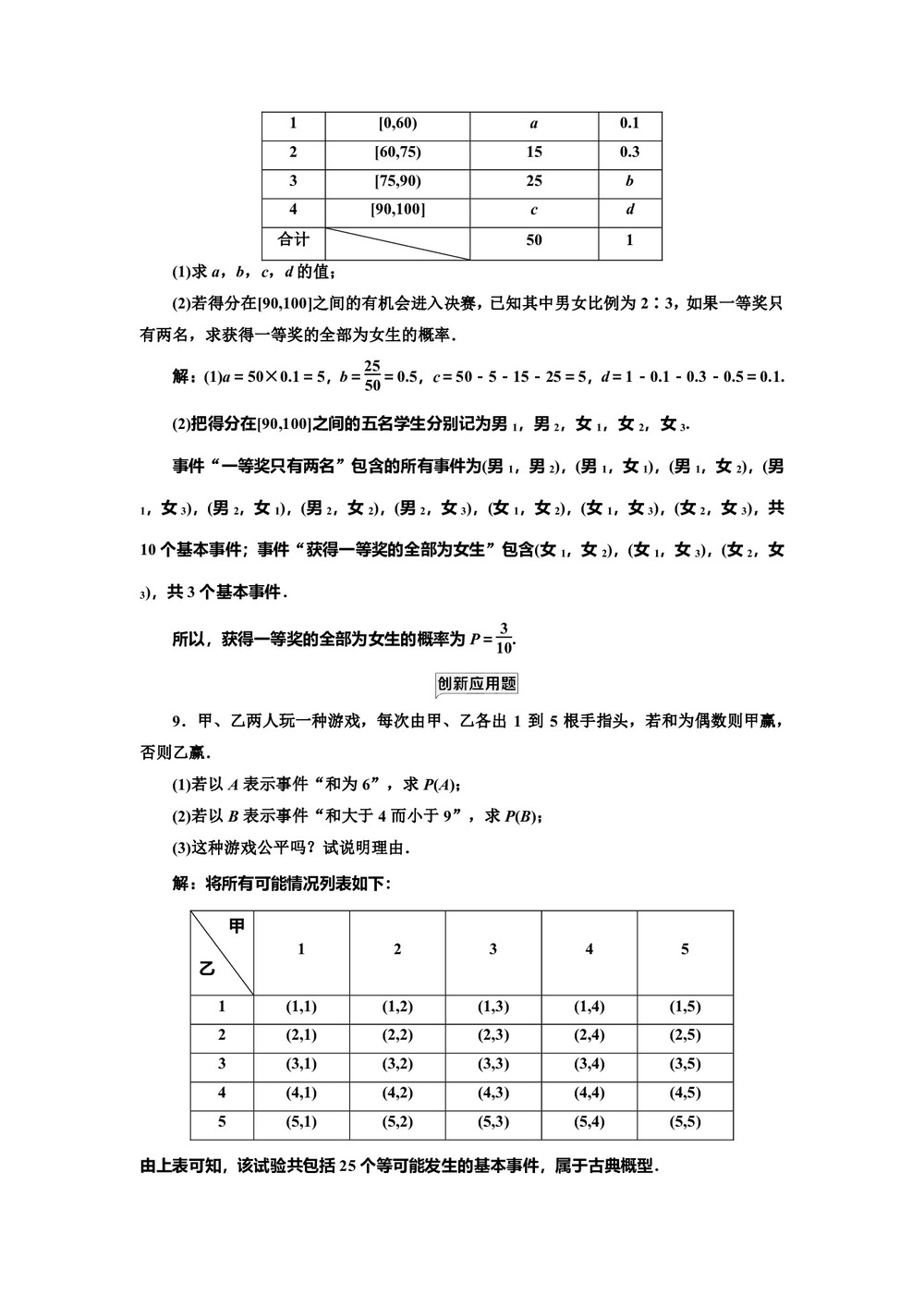
1 [0,60) a 0.1 2 [60,75) 15 0.3 3 [75,90) 25 b 4 [90,100] c d 合计 50 1 　　(1)求a，b，c，d的值；

　　(2)若得分在[90,100]之间的有机会进入决赛，已知其中男女比例为2∶3，如果一等奖只有两名，求获得一等奖的全部为女生的概率．

　　解：(1)a＝50×0.1＝5，b＝＝0.5，c＝50－5－15－25＝5，d＝1－0.1－0.3－0.5＝0.1.

　　(2)把得分在[90,100]之间的五名学生分别记为男1，男2，女1，女2，女3.

　　事件"一等奖只有两名"包含的所有事件为(男1，男2)，(男1，女1)，(男1，女2)，(男1，女3)，(男2，女1)，(男2，女2)，(男2，女3)，(女1，女2)，(女1，女3)，(女2，女3)，共10个基本事件；事件"获得一等奖的全部为女生"包含(女1，女2)，(女1，女3)，(女2，女3)，共3个基本事件．

　　所以，获得一等奖的全部为女生的概率为P＝.

　　9．甲、乙两人玩一种游戏，每次由甲、乙各出1到5根手指头，若和为偶数则甲赢，否则乙赢．

　　(1)若以A表示事件"和为6"，求P(A)；

　　(2)若以B表示事件"和大于4而小于9"，求P(B)；

　　(3)这种游戏公平吗？试说明理由．

　　解：将所有可能情况列表如下：

甲

乙 1 2 3 4 5 1 (1,1) (1,2) (1,3) (1,4) (1,5) 2 (2,1) (2,2) (2,3) (2,4) (2,5) 3 (3,1) (3,2) (3,3) (3,4) (3,5) 4 (4,1) (4,2) (4,3) (4,4) (4,5) 5 (5,1) (5,2) (5,3) (5,4) (5,5) 由上表可知，该试验共包括25个等可能发生的基本事件，属于古典概型．