【教学目标】

1.知识与技能：

　　掌握应用指数型，拟合型函数模型解答实际应用问题的题型特征，提升学生解决简单的实际应用问题的能力.

　　 2.过程与方法：经历实际应用问题的求解过程，体验指数函数模型、拟合函数模型的题型特征，学会运用函数知识解决实际问题.

3.情感态度价值观：

　　了解数学知识 于生活，又服务于实际，从而培养学生的数学应用意识，提高学生学习数学的兴趣.

【重点难点】

1.教学重点：指数函数模型、拟合函数模型的应用；

2.教学难点：依据题设情境，建立函数模型.

【教学策略与方法】

1.教学方法：合作探究、启发诱导，学生动手尝试相结合.

　　2.教具准备：多媒体

【教学过程】

教学流程 教师活动 学生活动 设计意图 环节一： 现实生活中有些实际问题所涉及的数学模型是确定的，但需我们利用问题中的数据及其蕴含的关系来建立. 对于已给定数学模型的问题，我们要对所确定的数学模型进行分析评价，验证数学模型的与所提供的数据的吻合程度.

问：对于幂函数、指数函数、对数函数，函数变化的速度有什么不同？

回答问题

复习上节知识，创设情境，引入课题。 环节二：

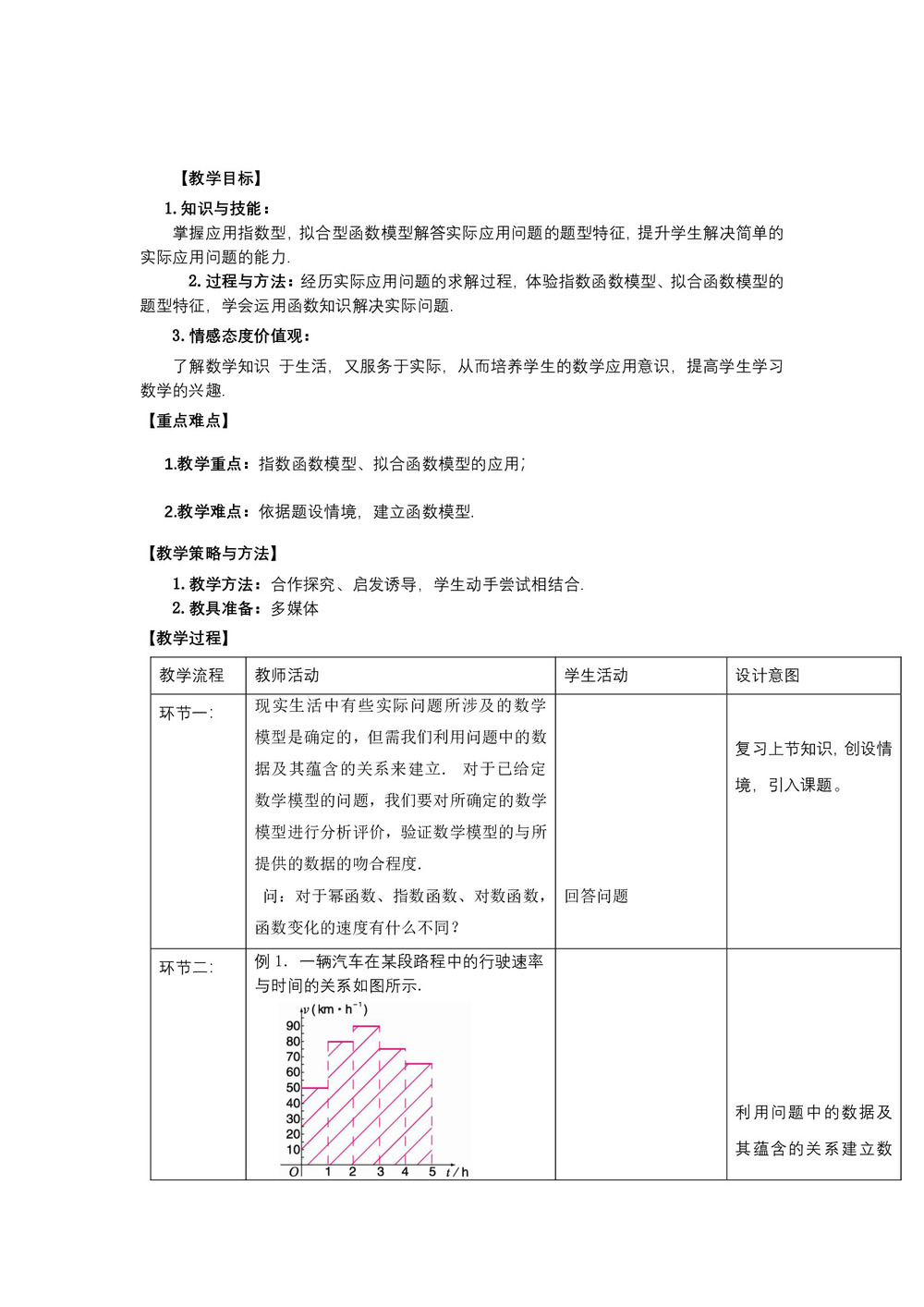
例1. 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.

（1）求图中阴影部分的面积，并说明所求面积的实际含义；

（2）假设这辆汽车行驶这段路程前的读数为2004 m，试建立行驶这段路程时汽车里程表读数s m与时间t h的函数关系式，并作出相应的图象.

探究： 1）你能写出速度v关于时间t的函数解析式吗?试试看！

2) 你能写出汽车行驶路程s关于时间t的函数解析式吗?试试看！

3) 你能作出s关于时间t的函数的图象吗?试试看

4)将图中的阴影部分隐去，得到的图象什么意义？

5）图中每一个矩形的面积的意义是什么？

6）汽车的行驶里程与里程表读数之间有什么关系？它们关于时间的函数图象又有何关系？

　　教师引导学生从条块图象的独立性思考问题，把握函数模型的特征.

解：（1）阴影部分的面积为

50×1+80×1+90×1+75×1+65×1=360

阴影部分的面积表示汽车在这5小时内行驶的路程为360 m.

（2） 根据图，有

这个函数的图象如图下所示.

例2. 人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律，可以为有效控制人口增长提供依据.早在1798年，英国经济学家马尔萨斯（T.R.Malthus，1766-1834）就提出了自然状态下的人口增长模型： y=y0ert,

其中t表示经过的时间，y0表示t=0时的人口数，r表示人口的年平均增长率.

下表是1950 1959年我国人口数据资料：

（1）如果以各年人口增长率的平均值作为我国这一时期的人口增长率（精确到0.0001），用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型，并检验所得模型与实际人口数据是否相符；

（2）如果按表的增长趋势，大约在哪一年我国的人口达到13亿？

探究：1）本例中所涉及的数量有哪些？

2）描述所涉及数量之间关系的函数模型是否是确定的，确定这种模型需要几个因素？

3）根据表中数据如何确定函数模型？

4）对于所确定的函数模型怎样进行检验，根据检验结果对函数模型又应作出如何评价？如何根据所确定函数模型具体预测我国某个时期的人口数，实质是何种计算方法？

解： （1）设1951 1959年的人口增长率分别为r1,r2,...,r9.由 55196（1+r1）=56300，

可得1951年的人口增长率 r1≈0.0200.

同理可得，

r2≈0.0210，r3≈0.0229，r4≈0.0250，

r5≈0.0197，r6≈0.0223，r7≈0.0276，

r8≈0.0222，r9≈0.0184.于是，1951 1959年期间，我国人口的年均增长率为 r=（r1+r2+... +r9）÷9≈0.0221.

令y0=55196，则我国在1950 1959年期间的人口增长模型为

y=55196e0.0221t，t∈N. 根据表中的数据作出散点图，并作出函数y=55196e0.0221t（t∈N）的图象（如下图）.

由上图可以看出，所得模型与1950 1959年的实际人口数据基本吻合.

（2）将y=130000代入

y=55196e0.0221t（t∈N），

由计算器可得 t≈38.76. 所以，如果按表的增长趋势，那么大约在1950年后的第39年（即1989年）我国的人口就已达到13亿.由此可以看到如果不实行计划生育，而是让人口自然增长，今天我国将面临难以承受的人口压力.

练习：课本104页 1、2题

例3 某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元.销售单价与日均销售量的关系如表所示：

销售单价/元 6 7 8 9 日均销售量/桶 480 440 400 360 销售单价/元 10 11 12 日均销售量/桶 320 280 240 请据以上数据作出分析，这个经营部怎样定价才能获得最大利润？

探究：1）你能看出表中的数据有什么变化规律？假设每桶水在进价的基础上增加x元，日均销售量为多少？

2) 设日均销售利润为y元，那么y与x的关系如何？

3) 上述关系表明，日均销售利润y元是x 的函数，那么这个函数的定义域是什么？

4) :这个经营部怎样定价才能获得最大利润？

5)

6)

7)

8)

9)

10)

11)

12)

13) 解：根据表，销售单价每增加1元，日均销售量就减少40桶.设在进价基础上增加x元后，日均销售利润为y 元，而在此情况下的日均销售量就为

480-40(x-1)=520-40x(桶)

由于x＞0且520-40x＞0，即0＜x＜13，于是可得

y=(520-40x)x-200

= -40x2+520x-200，0＜x＜13

易知，当x=6.5时，y有最大值.

所以，只需将销售单价定为11.5元，就可获得最大的利润.

思考：你能总结一下用函数解决应用性问题中的最值问题的一般思路吗？

例4 某地区不同身高的未成年男性的体重平均值如表

身高/cm 60 70 80 90 100 110 体重/ g 6.13 7.90 9.90 12.15 15.02 17.50 身高/cm 120 130 140 150 160 170 体重/ g 20.92 26.86 31.11 38.85 47.25 55.05 （1）根据表提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重y g与身高xcm的函数关系？试写出这个函数模型的解析式.

（2）若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为175cm，体重为78 g的在校男生的体重是否正常？

探究;1）上表提供的数据对应的散点图大致如何？

2） 根据这些点的分布情况，可以选用那个函数模型进行拟合，使它能比较近似地反映这个地区未成年男性体重与身高的函数关系？

3） 如何求出函数关系式中参数a,b？

解：（1）以身高为横坐标，体重为纵坐标，画出散点图.根据点的分布特征，可考虑以y=a·bx作为刻画这个地区未成年男性的体重与身高关系的函数模型.

如果取其中的两组数据(70，7.90)，(160，47.25)，代入y=a·bx得：，用计算器算得a≈2，b≈1.02.

这样，我们就得到一个函数模型：y=2×1.02x.

将已知数据代入上述函数解析式，或作出上述函数的图象，可以发现，这个函数模型与已知数据的拟合程度较好，这说明它能较好地反映这个地区未成年男性体重与身高的关系.

（2）将x=175代入y=2×1.02x得y=2×1.02175，

由计算器算得y≈63.98.

由于78÷63.98≈1.22＞1.2，

所以，这个男生偏胖.

思考4:这个例题有什么特点？

此类问题由数据不能直接得出确定的函数模型，需要画散点图，通过图象特点选择合适的函数模型，再通过代入点的坐标求出近似模型，再对实际问题作出预测

思考5:你能总结一下用拟合函数解决应用性问题的基本过程吗？

学生感悟体验，思考回答。

先让学生尝试着解答本题。

学生互相交流，回答补充

学生独立完成，代表板演。

学生回答问题

学生板演解题步骤

学生独立画图，思考问题，代表回答。

在老师的引导下审题、建模、求解、检验、尝试完成此例

小组讨论，总结

利用问题中的数据及其蕴含的关系建立数学模型．此题的主要意图是让学生用函数模型（分段函数）刻画实际问题．

问题的引导可以使学生更好的把握问题的关键。

通过实例求解，提炼方法整合思路提升能力.

让学生验证问题中的数据与所提供的数学模型是否吻合，并用数学模型解释实际问题，并利用模型进行预测。

以旧引新激发兴趣，再现应用技能.

通过学生的板演，规范解题步骤。

通过实例求解，提炼方法整合思路提升能力.

总结解题思路，提高解题能力。