2019-2020学年苏教版选修2-2 　导数的几何意义 教案

【教学重点】：

　　理解曲线在一点处的切线的定义，以及曲线在一点处的切线的斜率的定义.光滑曲线的切线斜率是了解导数概念的实际背景．导数的几何意义及"数形结合，以直代曲"的思想方法.

【教学难点】：

　　发现、理解及应用导数的几何意义,会求一条具体的曲线在某一点处的切线斜率.

【教学过程设计】：

教学环节 教学活动 设计意图 一、曲线的切线及切线的斜率： 　　圆与圆锥曲线的切线定义：与曲线只有一个公共点并且位于曲线一边的直线叫切线。

曲线的切线

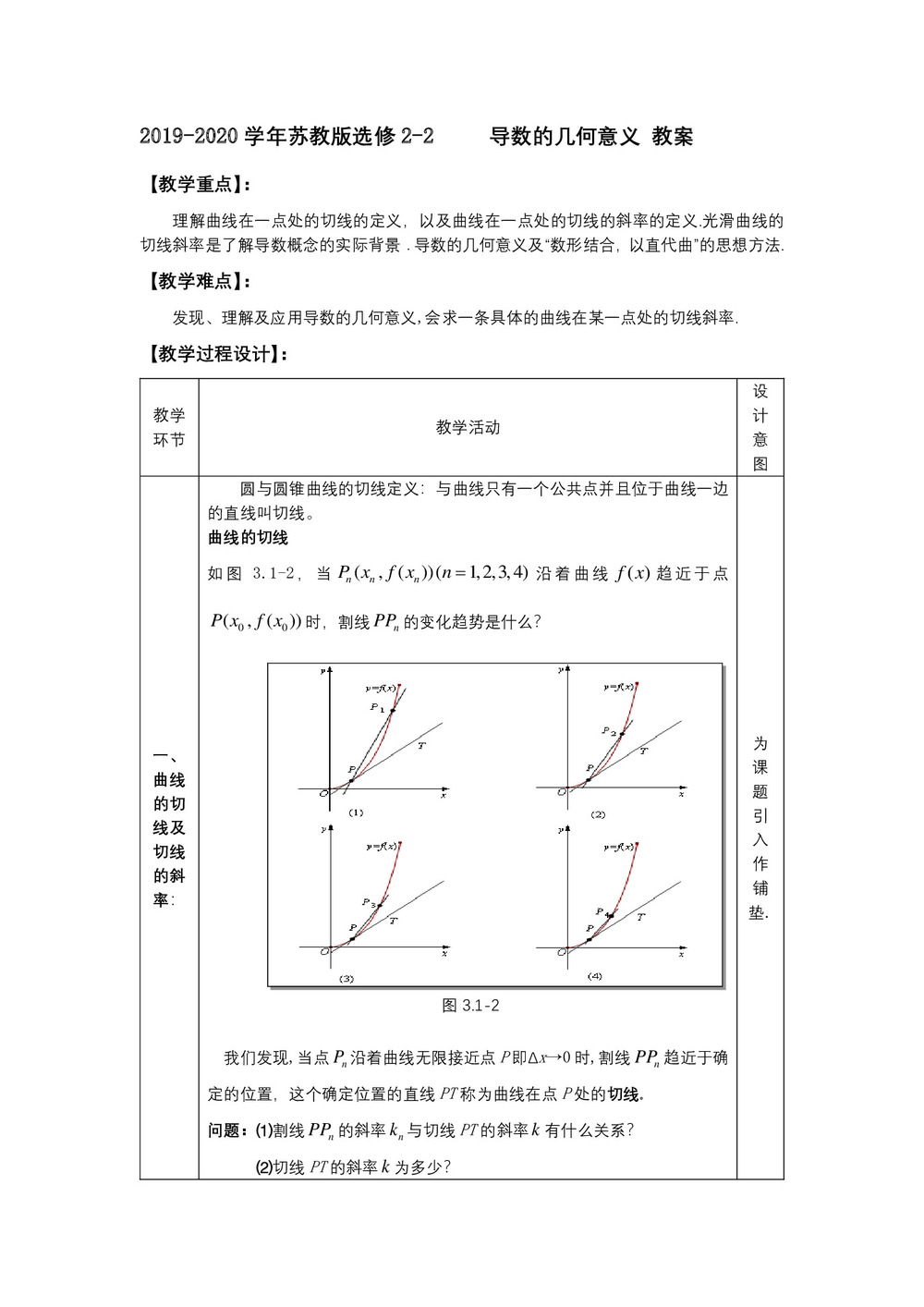
如图3.1-2，当沿着曲线趋近于点时，割线的变化趋势是什么？

　我们发现,当点沿着曲线无限接近点P即Δx→0时,割线趋近于确定的位置，这个确定位置的直线PT称为曲线在点P处的切线.

问题：⑴割线的斜率与切线PT的斜率有什么关系？

⑵切线PT的斜率为多少？

容易知道，割线的斜率是,当点沿着曲线无限接近点P时，无限趋近于切线PT的斜率，即

说明：（1）设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.

这个概念: ①提供了求曲线上某点切线的斜率的一种方法;

②切线斜率的本质-函数在处的导数.

（2）曲线在某点处的切线:1)与该点的位置有关;2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个. 为课题引入作铺垫.