如何判别f(x0)是极大、极小值 填空：

（1）若满足，且在的两侧的导数________，则是的极值点，是极值，

（2）如果在两侧满足"左正右负"，则是的_______点，是_______；

（3）如果在两侧满足"左负右正"，则是的_______点，是_______.

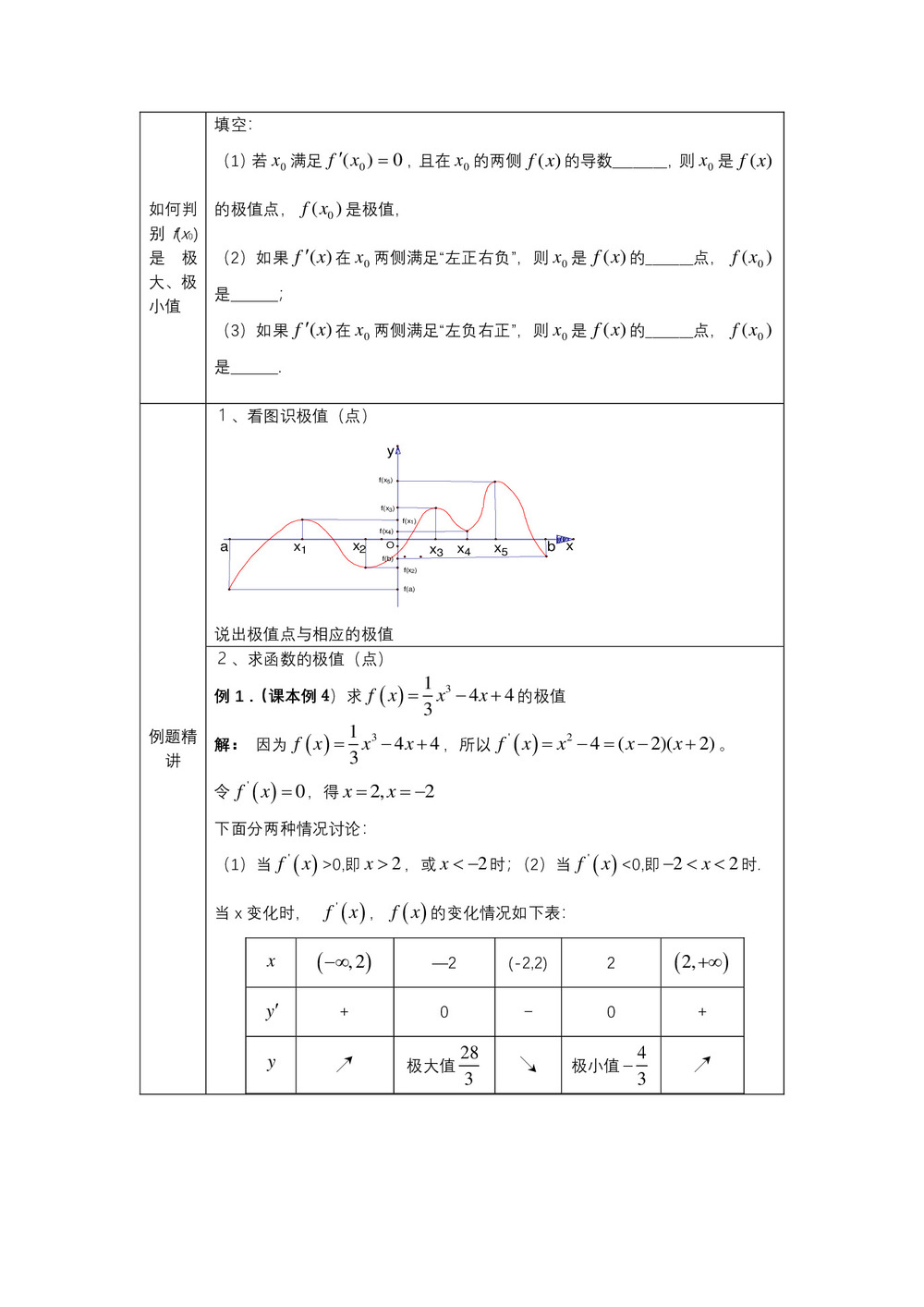
　　 例题精讲 １、看图识极值（点）

说出极值点与相应的极值 ２、求函数的极值（点）

例1．（课本例4）求的极值

解： 因为，所以。

令，得

下面分两种情况讨论：

（1）当>0,即，或时；（2）当<0,即时.

当x变化时， ，的变化情况如下表：

-2 (-2,2) 2 + 0 － 0 + ↗ 极大值 ↘ 极小值 ↗

因此，=；

=。

函数的图像如图所示。

对教材例1的处理方式：

要求阅读教材解析，模仿练习。以眼动、心动、手动的方式让学生对求解函数的极值的步骤有较深的印象。

例2、求y=(x2－1)3+1的极值

解：y′=6x(x2－1)2=6x(x+1)2(x－1)2, 令y′=0解得x1=－1，x2=0，x3=1

当x变化时，y′，y的变化情况如下表

-1 (-1,0) 0 (0,1) 1 － 0 － 0 + 0 + ↘ 无极值 ↘ 极小值0 ↗ 无极值 ↗ ∴当x=0时，y有极小值且y极小值=0

例3、 设，在和处有极值，且=－1,求，，的值，并求出相应的值。

解：，∵是函数的极值点，则－1,1是方程的根，即有⇒，又，则有，由上述三个方程可知，，，此时，函数的表达式为，∴，令，得，当变化时，，的变化情况表：

-1 (-1,1) 1 + 0 － 0 + ↗ 极大值1 ↘ 极小值

－1 ↗ 由上表可知， ，