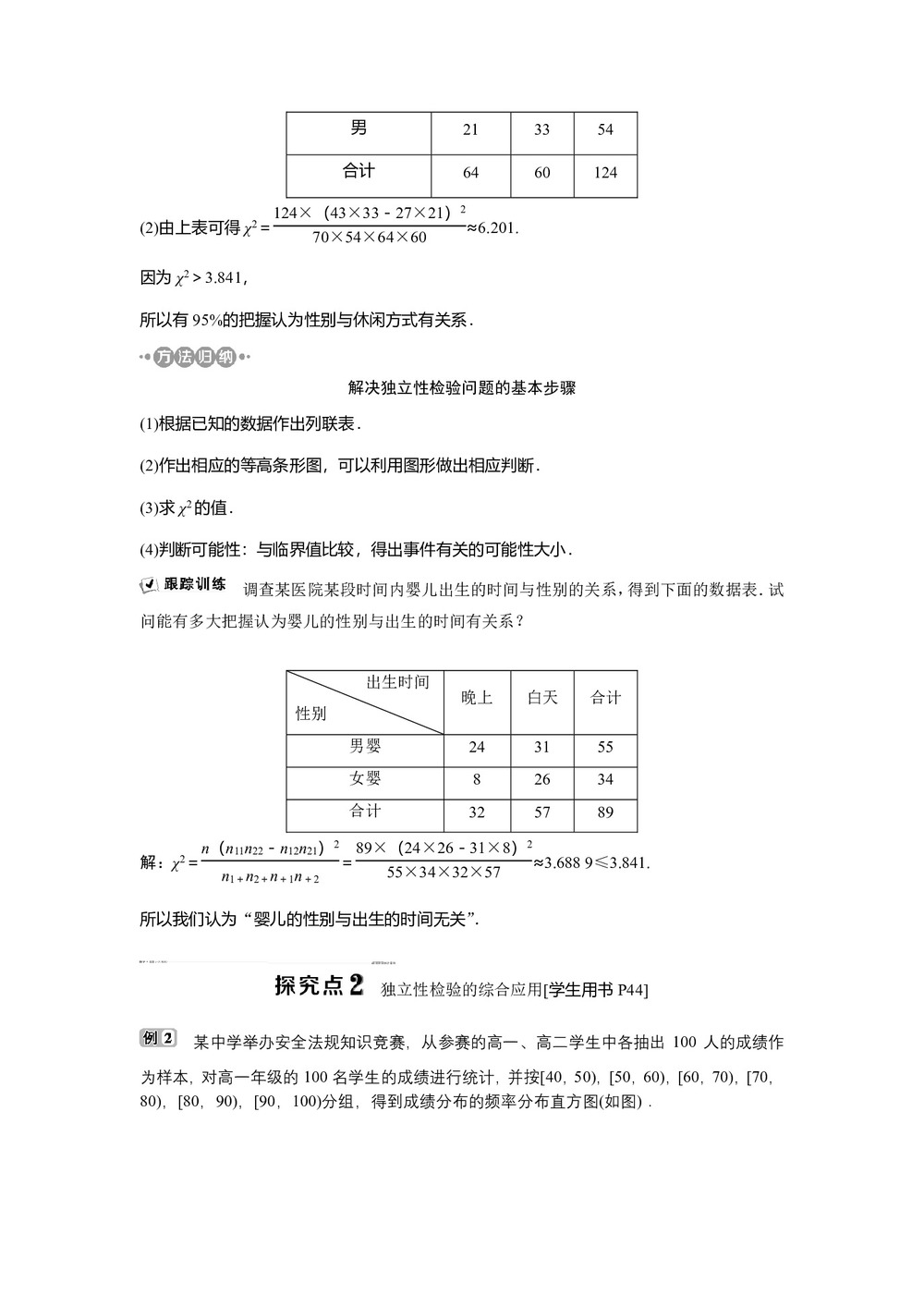
男 21 33 54 合计 64 60 124 (2)由上表可得χ2＝≈6.201.

因为χ2＞3.841，

所以有95%的把握认为性别与休闲方式有关系．

解决独立性检验问题的基本步骤

(1)根据已知的数据作出列联表．

(2)作出相应的等高条形图，可以利用图形做出相应判断．　

(3)求χ2的值．

(4)判断可能性：与临界值比较，得出事件有关的可能性大小．

　调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表．试问能有多大把握认为婴儿的性别与出生的时间有关系？

　　　　出生时间

性别　　　　 晚上 白天 合计 男婴 24 31 55 女婴 8 26 34 合计 32 57 89 解：χ2＝＝≈3.688 9≤3.841.

所以我们认为"婴儿的性别与出生的时间无关"．

　独立性检验的综合应用[学生用书P44]

　某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本，对高一年级的100名学生的成绩进行统计，并按[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100)分组，得到成绩分布的频率分布直方图(如图)．