2.5随机变量的均值与方差
前面所讨论的随机变量的取值都是离散的,我们把这样的随机变量称为离散型随机变量。怎样刻画离散型随机变量取值的平均水平和稳定程度呢?
2.5.1离散型随机变量的均值
1、通过实例,理解有限值的离散型随机变量的均值(数学期望)的概念和意义;
2、会提出、分析、解决带有实际意义或与生活有联系的数学问题;提高用均值的数学语言表达问题进行交流的能力;
3、要引导学生接触自然,了解社会,参加形式多样的实践活动,使学生接触自然,了解社会,参加形式多样的实践活动,使学生对自然界和社会中的数学现象具有好奇心,有追求新知的欲望,能够独立思考,会从数学的角度发现和指出问题并加以探索和研究。
【教学过程】
一、问题引入:
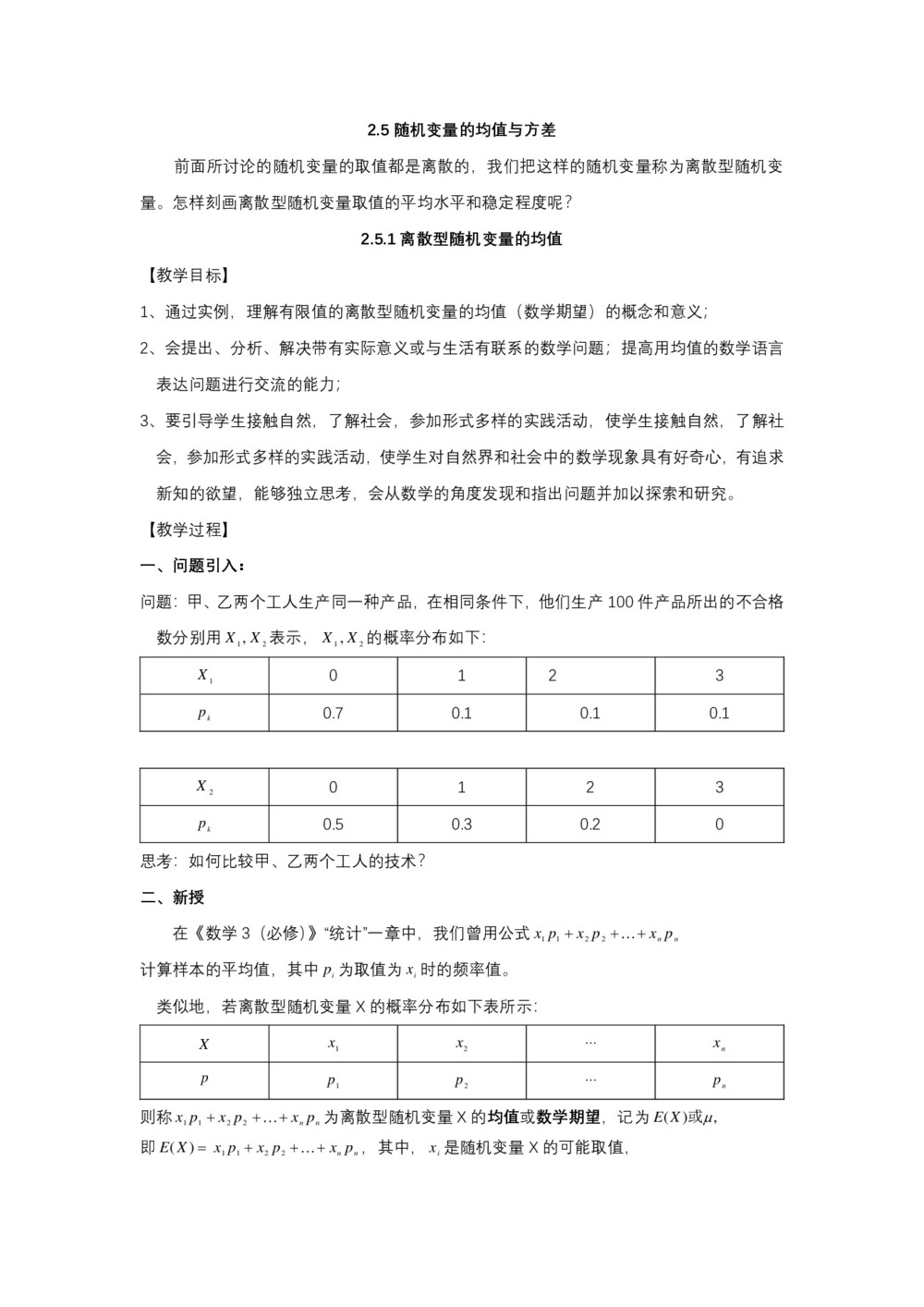
问题:甲、乙两个工人生产同一种产品,在相同条件下,他们生产100件产品所出的不合格数分别用表示,的概率分布如下:
0 1 2 3 0.5 0.3 0.2 0 思考:如何比较甲、乙两个工人的技术?
二、新授
在《数学3(必修)》"统计"一章中,我们曾用公式
计算样本的平均值,其中为取值为时的频率值。
类似地,若离散型随机变量X的概率分布如下表所示:
... ... 则称为离散型随机变量X的均值或数学期望,记为
即,其中,是随机变量X的可能取值,
-
相关教案下载
- 12019-2020学年北师大版选修2-3 离散型随机变量的均值与方差 教案
- 22019-2020学年北师大版选修2-3 2.5 离散型随机变量的均值与方差 教案
- 32019-2020学年北师大版选修2-3 离散型随机变量的期望与方差(二) 教案
- 42019-2020学年北师大版选修2-3 离散型随机变量的方差 教案
- 52018-2019学年北师大版选修2-3 离散型随机变量的方差 教案
- 62018-2019学年北师大版选修2-3 离散型随机变量的均值 教案
- 72017-2018学年北师大版选修2-3 离散型随机变量的均值 教案
- 82019-2020学年北师大版选修2-3 随机变量 教案
- 92017-2018学年北师大版选修2-3 离散型随机变量的方差 教案