生：（可能会回答）

师：这是一个定积分的性质：（其中）．

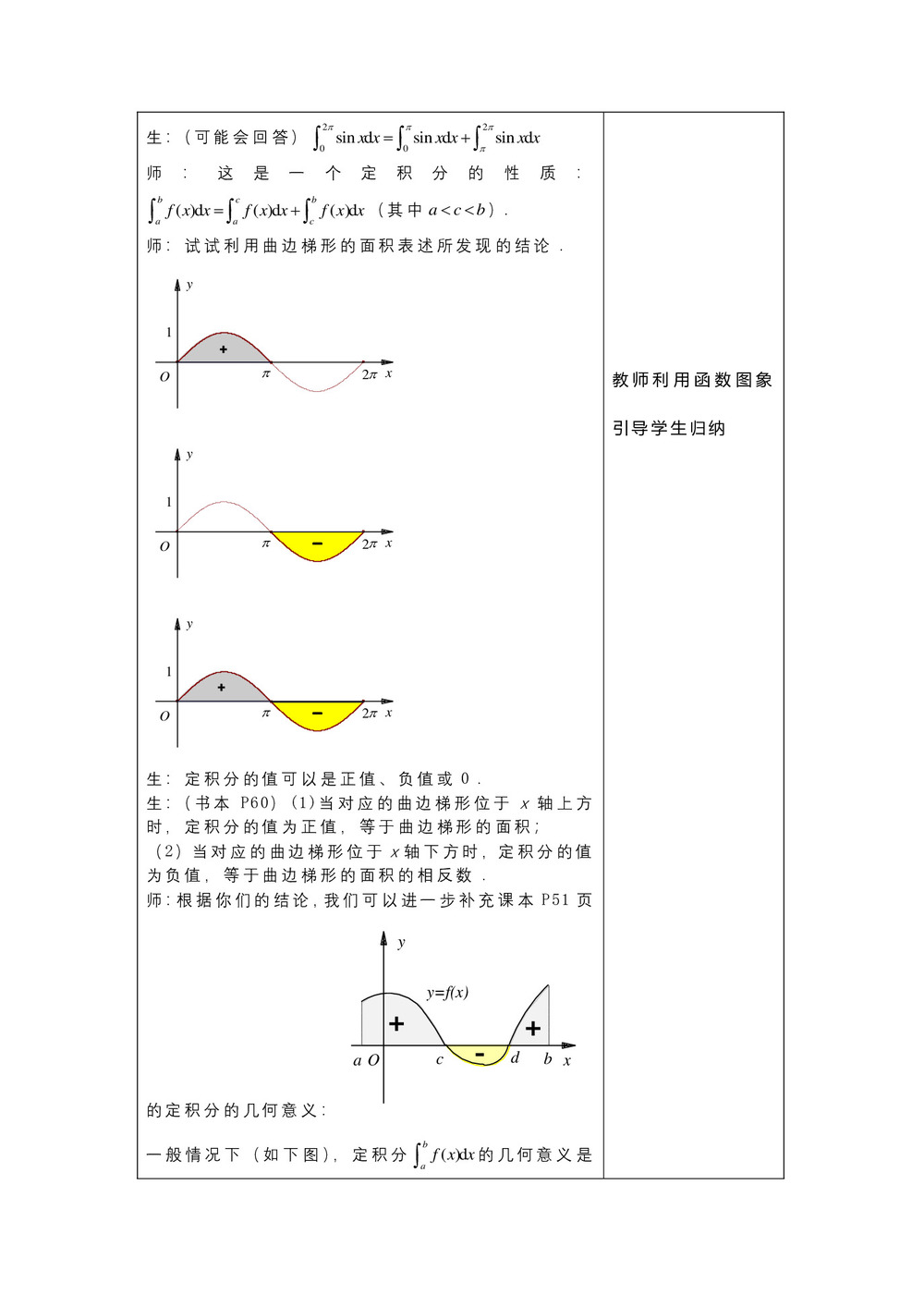
师：试试利用曲边梯形的面积表述所发现的结论．

生：定积分的值可以是正值、负值或0．

生：（书本P60）(1)当对应的曲边梯形位于x轴上方时，定积分的值为正值，等于曲边梯形的面积；

（2）当对应的曲边梯形位于x轴下方时，定积分的值为负值，等于曲边梯形的面积的相反数．

师：根据你们的结论，我们可以进一步补充课本P51页的定积分的几何意义：

一般情况下（如下图），定积分的几何意义是介于x轴、函数的图象以及直线之间各部分面积的代数和，在x轴上方的面积取正号；在x轴下方的面积取负号．

师：如果在区间上恒为正，则定积分，为面积值；但是，不能推出在区间上恒为正．

师：由上图我们还可以等出一个结论：

若在区间上不是恒为非负的，则函数与x轴以及直线所围的图形的面积为．例如上图中，

例题3：已知在上连续，若是奇函数，则 ．并证明你的结论。

附证明：（1）∵在上连续,是奇函数，

∴，

设，则有,

∴（C为常数）

令，则有，∴

∴

∴

∴原式得证

师：本题从几何直观上是非常容易理解的，但是要使用微积分基本定理证明，关键是证明奇函数的原函数是偶函数这个性质．

教师利用函数图象引导学生归纳

给出一般结论

着重说明定积分的值与曲边梯形面积之间的关系：令位于x轴上方的曲边梯形的面积取正值，位于x轴下方的曲边梯形的面积取负值，这样定积分的值就是曲边梯形面积的代数和

显示出数形结合的威力

复合函数的求导法则的逆运用

容易误为

再次强调运用微积分基本定理求定积分的关键是求出原函数F(x)