利用教材在§3.3.1中的例1引入函数的极值概念

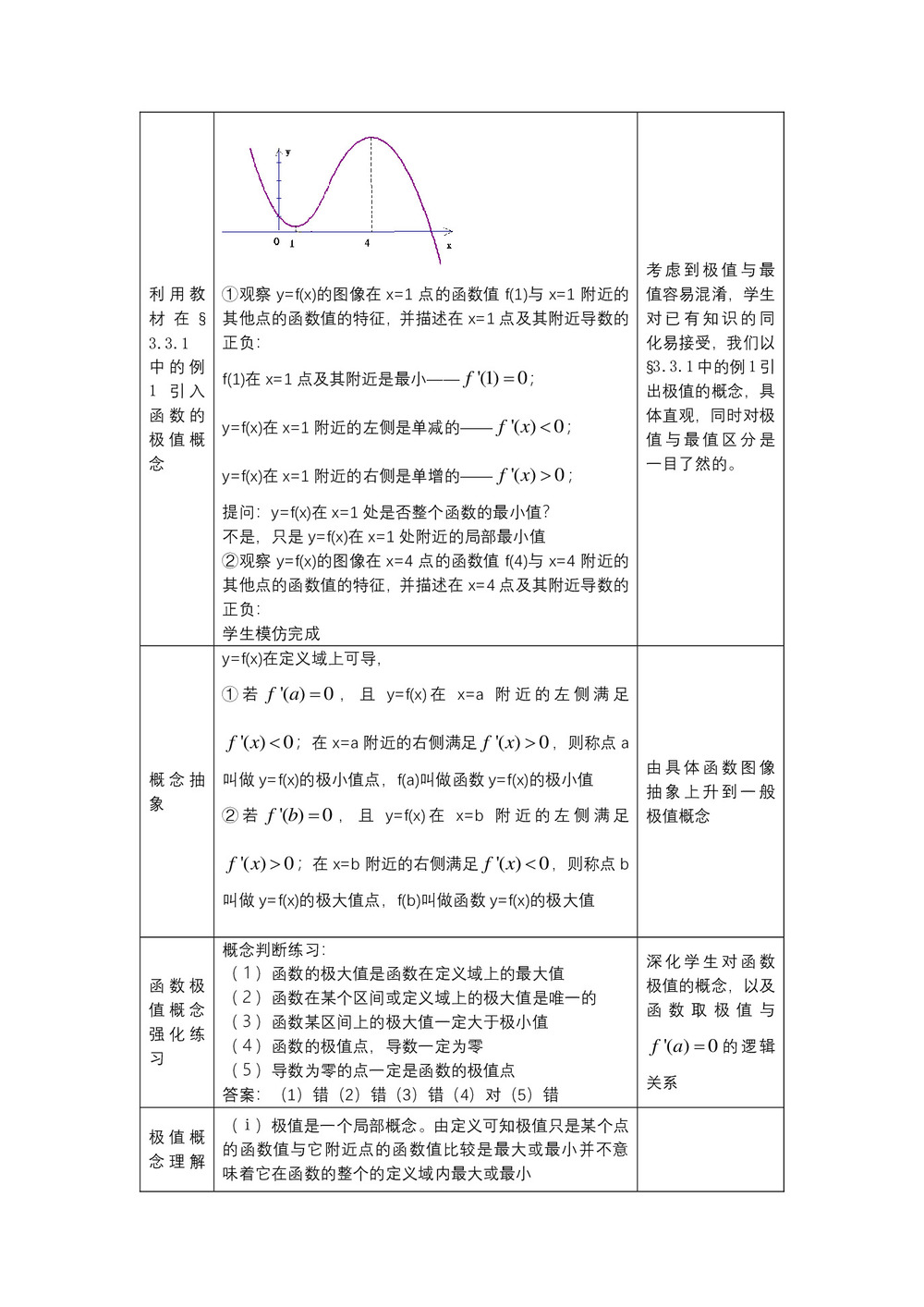
①观察y=f(x)的图像在x=1点的函数值f(1)与x=1附近的其他点的函数值的特征，并描述在x=1点及其附近导数的正负：

f(1)在x=1点及其附近是最小--；

y=f(x)在x=1附近的左侧是单减的--；

y=f(x)在x=1附近的右侧是单增的--；

提问：y=f(x)在x=1处是否整个函数的最小值？

不是，只是y=f(x)在x=1处附近的局部最小值

②观察y=f(x)的图像在x=4点的函数值f(4)与x=4附近的其他点的函数值的特征，并描述在x=4点及其附近导数的正负：

学生模仿完成 考虑到极值与最值容易混淆，学生对已有知识的同化易接受，我们以§3.3.1中的例1引出极值的概念，具体直观，同时对极值与最值区分是一目了然的。

概念抽象 y=f(x)在定义域上可导，

①若，且y=f(x)在x=a附近的左侧满足；在x=a附近的右侧满足，则称点a叫做y=f(x)的极小值点，f(a)叫做函数y=f(x)的极小值

②若，且y=f(x)在x=b附近的左侧满足；在x=b附近的右侧满足，则称点b叫做y=f(x)的极大值点，f(b)叫做函数y=f(x)的极大值

由具体函数图像抽象上升到一般极值概念 函数极值概念强化练习 概念判断练习：

（１）函数的极大值是函数在定义域上的最大值

（２）函数在某个区间或定义域上的极大值是唯一的

（３）函数某区间上的极大值一定大于极小值

（４）函数的极值点，导数一定为零

（５）导数为零的点一定是函数的极值点

答案：（1）错（2）错（3）错（4）对（5）错 深化学生对函数极值的概念，以及函数取极值与的逻辑关系 极值概念理解的总结提高 （ⅰ）极值是一个局部概念。由定义可知极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小

（ⅱ）函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个

（ⅲ）极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值，如下图所示，是极大值点，是极小值点，而>，如下图

如何判别f(x0)是极大、极小值 填空：

（1）若满足，且在的两侧的导数________，则是的极值点，是极值，

（2）如果在两侧满足"左正右负"，则是的_______点，是_______；

（3）如果在两侧满足"左负右正"，则是的_______点，是_______.

　　 让学生总结判断极值的方法。

（１）异号；（２）极大值；极大值；

（３）极小值；极小值