所以，所求切线的斜率为6，因此，所求的切线方程为即

例2、求曲线f(x)=x3－x2+5在x=1处的切线的倾斜角.

　　分析：要求切线的倾斜角，也要先求切线的斜率，再根据斜率k=tana，求出倾斜角a.

解：∵tana=

　　∵a∈［0，π，∴a=π.

　　∴切线的倾斜角为π.

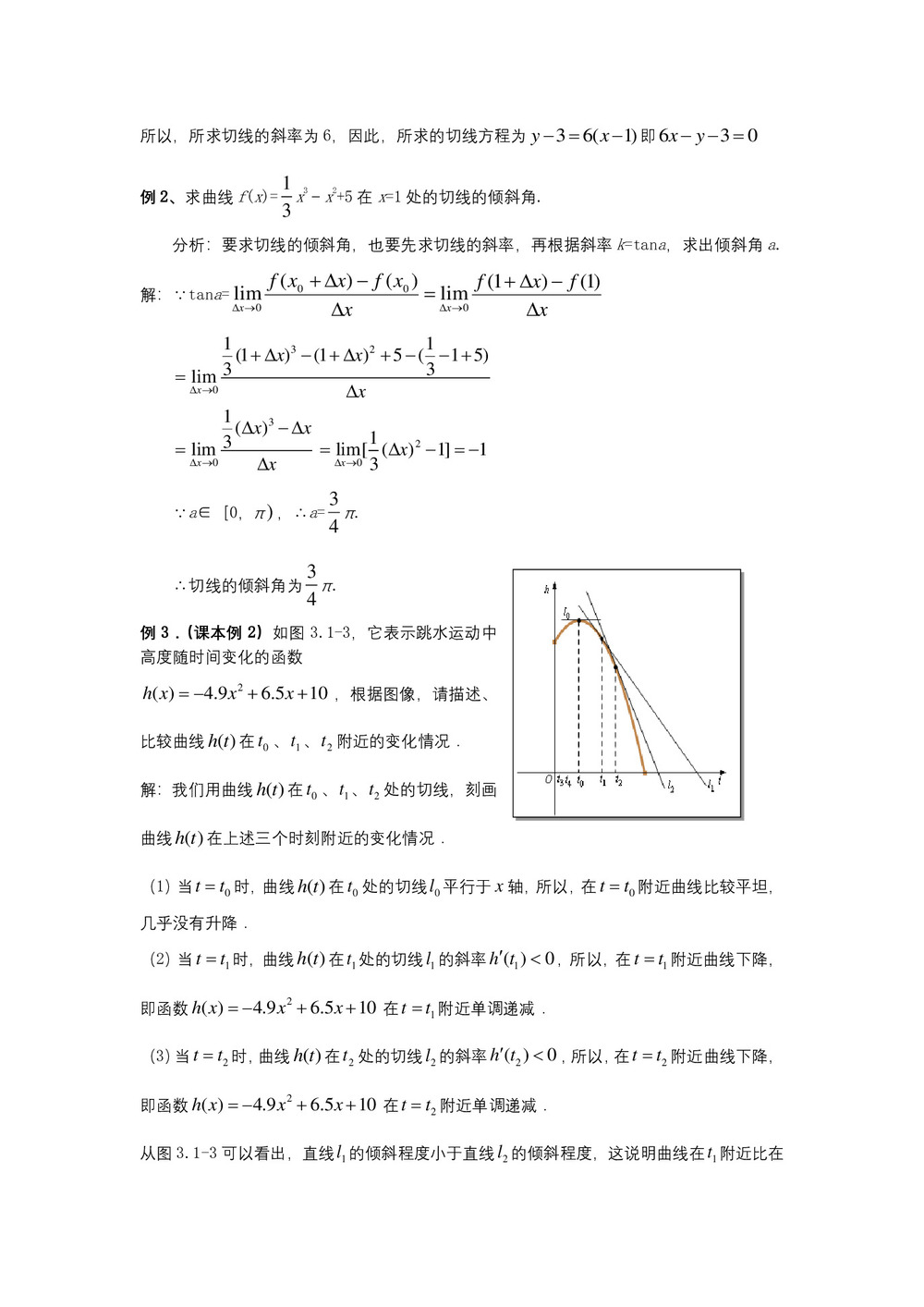
例3．（课本例2）如图3.1-3，它表示跳水运动中高度随时间变化的函数

，根据图像，请描述、比较曲线在、、附近的变化情况．

解：我们用曲线在、、处的切线，刻画曲线在上述三个时刻附近的变化情况．

（1）当时，曲线在处的切线平行于轴，所以，在附近曲线比较平坦，几乎没有升降．

（2）当时，曲线在处的切线的斜率，所以，在附近曲线下降，即函数在附近单调递减．

（3）当时，曲线在处的切线的斜率，所以，在附近曲线下降，即函数在附近单调递减．

从图3.1-3可以看出，直线的倾斜程度小于直线的倾斜程度，这说明曲线在附近比在附近下降的缓慢．